Understanding Community Detection
What is Community Detection?
Picture a Social Network: Imagine a large social media network as a graph. People are the nodes (dots), and friendships are the edges (lines connecting the dots). Community detection is like finding the “cliques” or tightly knit groups within this massive web of connections. Community detection is a fundamental topic in network analysis, aiming to identify groups of nodes within a network that are more densely connected with each other than with nodes outside the group.
Why Is It Important?
Community detection can help in many ways, such as understanding social networks (like finding groups within Facebook friends), making recommendations (like suggesting movies on Netflix based on what similar users like), or even in biology (like finding groups of genes that work together).
A Simple Algorithm: Girvan-Newman
The Girvan-Newman algorithm works by finding and removing the weakest connections between groups, slowly revealing the natural divisions within the network. It’s like removing the least important bridges to see which islands of friends emerge.
Getting Started with Python
First, we need to set up our tools. We’ll use a Python library called NetworkX for this. If you don’t have it yet, you can install it like this:
pip install networkx
Now, let’s create a simple network and apply the Girvan-Newman algorithm to detect communities within this network.
Step 1: Import Libraries
import networkx as nx
import matplotlib.pyplot as plt
from networkx.algorithms.community import girvan_newman
Step 2: Create a Network
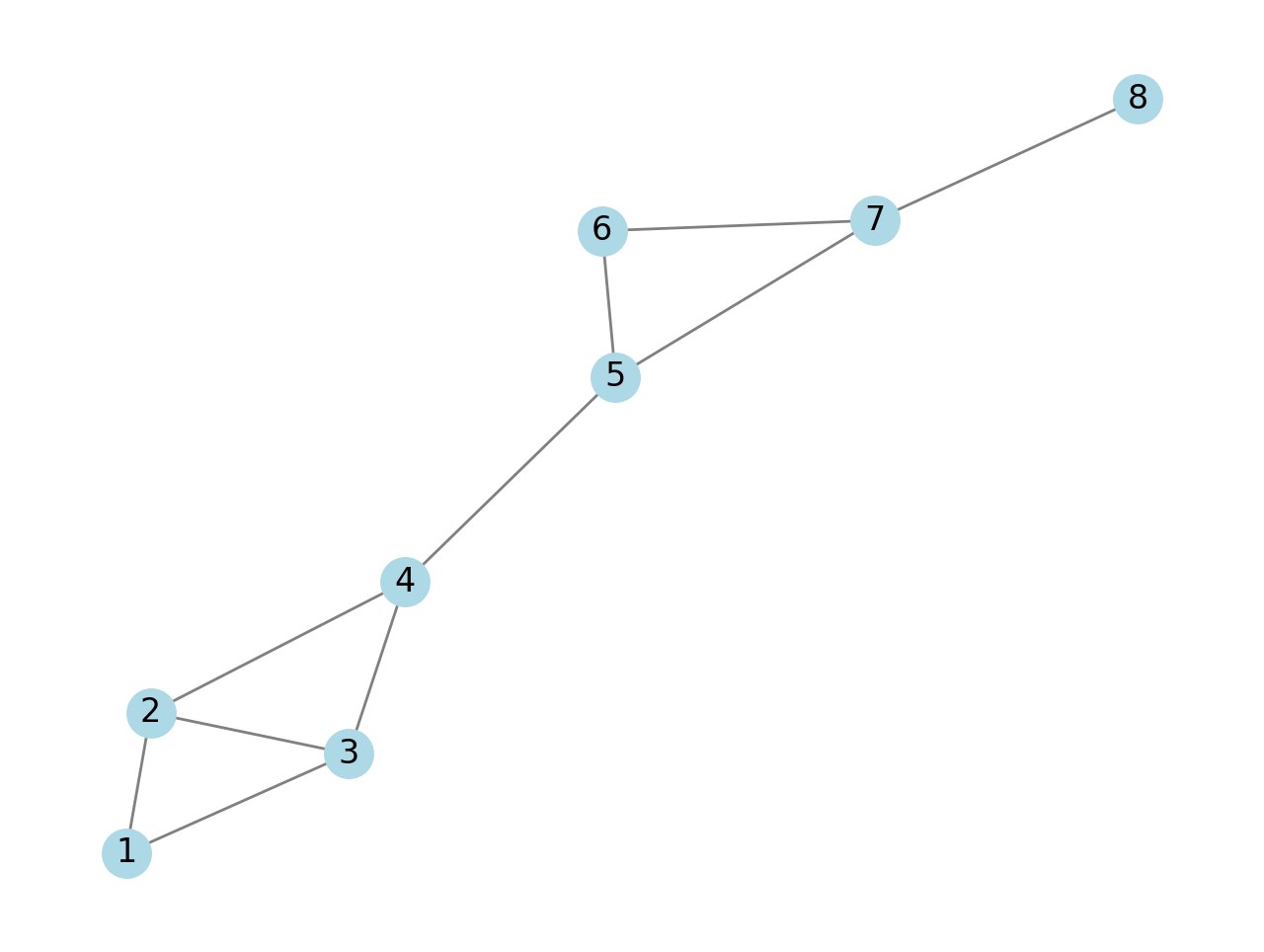
For this example, we’ll create a small network with some connections.
# Create a new graph
G = nx.Graph()
# Add nodes
G.add_nodes_from(range(1, 9))
# Add edges (connections)
edges = [(1, 2), (1, 3), (2, 3), (2, 4), (3, 4), (4, 5), (5, 6), (5, 7), (6, 7), (7, 8)]
G.add_edges_from(edges)
# Draw the network
nx.draw(G, with_labels=True, node_color='lightblue', edge_color='gray')
plt.show()
This code creates and draws a simple network of 8 nodes with specific connections.
Step 3: Apply the Girvan-Newman Algorithm
# Apply the Girvan-Newman algorithm
communities = list(girvan_newman(G))
# Print the communities
for i, community in enumerate(communities):
print(f"Community {i}: {list(community)}")
This code applies the Girvan-Newman algorithm to the network. The girvan_newman function returns an iterator over communities at each level of the algorithm. For simplicity, we convert it to a list and print the communities.
Step 4: Understanding the Output
The output will be a list of community groupings at each level of edge removal. Each grouping shows how the network divides into communities as the algorithm progresses.
Community 0
{1, 2, 3, 4}{8, 5, 6, 7}
Community 1
{1, 2, 3, 4}{5, 6, 7}{8}
Community 2
{1}{2, 3, 4}{5, 6, 7}{8}
Community 3
{1}{2}{3, 4}{5, 6, 7}{8}
Community 4
{1}{2}{3}{4}{5, 6, 7}{8}
Community 5
{1}{2}{3}{4}{5}{6, 7}{8}
Community 6
{1}{2}{3}{4}{5}{6}{7}{8}-
Community 0: The network is initially divided into two communities. This division represents the broadest distinction within the network, identifying two core groups that are more connected internally than they are to each other.
-
Community 1: As the algorithm progresses, one of the communities is further divided, showing a finer level of structure within the network. This indicates that within one of the initial communities, there is a subgroup that has its own distinct set of connections.
-
Communities 2 to 6: Each subsequent division represents a continued refinement in identifying communities within the network. The algorithm uncovers smaller and more specific groups of nodes that are closely connected, indicating layers of community structure.
- Community 6: Finally, every node is considered its own community. This represents the most refined level of division possible and indicates that all bridges connecting distinct groups have been removed.