What are Graphs?

Imagine a network of cities connected by roads. In graph theory, we turn this into a simplified model:

  • Cities become vertices (or nodes): These are just dots representing the objects. Alt text for the image

  • Roads become edges: Lines connecting the dots show relationships between the objects. Alt text for the image

Graphs help us model all sorts of things: social media networks (people are nodes, friendships are edges), molecule structures, or even the layout of a website.

Types of Graphs

  • Directed vs. Undirected:
    • Undirected: Roads are two-way streets (think friendship on Facebook). Alt text for the image
    • Directed: Roads are one-way streets (think following someone on Twitter). Alt text for the image
  • Weighted vs. Unweighted:
    • Unweighted: Roads are all the same; edges simply show if a connection exists.
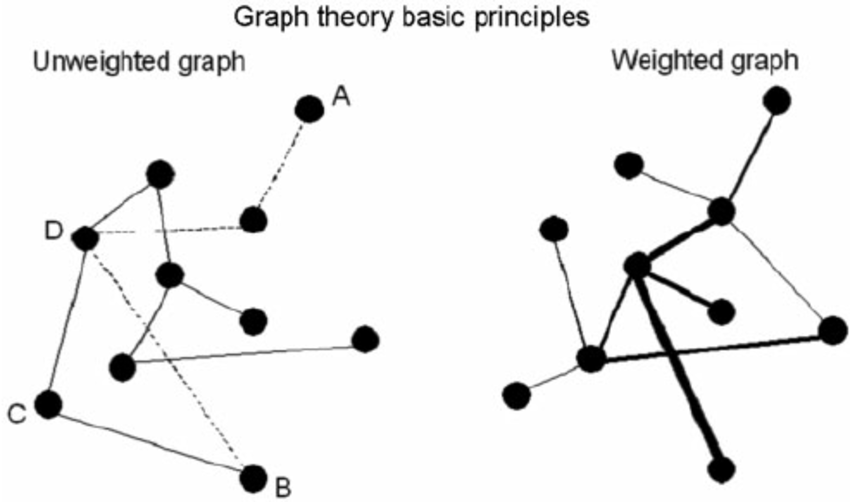
    • Weighted: Roads have distances or costs (think airline routes). Alt text for the image

Key Concepts

  • Degree of a Vertex: How many edges are connected to a single vertex (how many roads lead to a city).

  • Path: A sequence of vertices connected by edges (like a route you’d take traveling between cities). Alt text for the image

  • Cycle: A path that starts and ends at the same vertex (imagine a roundtrip road trip).

Representing Graphs

To work with graphs in computers, we need ways to store their structure:

  • Adjacency Matrix: Think of it as a table: Imagine you have a small town with four streets (let’s call them A, B, C, and D). Here’s how an adjacency matrix would represent which streets connect:

      ```
  A  B  C  D
  A  0  1  0  1
  B  1  0  1  0
  C  0  1  0  1
  D  1  0  1  0 
  ```
    • Table Layout: The top row and the leftmost column list the street names.
    • Reading the Matrix: If there’s a ‘1’ at the intersection of a row and column, there’s a connection.
    • Example: Street ‘A’ is connected to street ‘B’ (row ‘A’, column ‘B’ has a ‘1’).
    • Example 2: Street ‘B’ is NOT connected to itself (row ‘B’, column ‘B’ has a ‘0’).

Visualizing the Adjacency Matrix Adjacency List

Think of it like each street having a list of its “neighbors”:

  • A: [B, D]
  • B: [A, C]
  • C: [B, D]
  • D: [A, C]

Visualizing the Adjacency List Which is Better?

  • Adjacency Matrix:
    • Fast to check if a specific connection exists (just look up the cell).
    • Can waste space if there are few connections (lots of ‘0’s in a big table).
  • Adjacency List:
    • More space-efficient for graphs where most things aren’t connected to each other.
    • Slower to check for specific connections (have to search through lists).